3 Free Math Worksheets Third Grade 3 Fractions and Decimals Subtracting Decimals In Columns 1 Digit – Welcome aboard the journey into the world of education printable worksheets in Math, English, Science and Social Studies, aligned with the CCSS but… Continue Reading →
3 Free Math Worksheets First Grade 1 Subtraction Subtracting whole Tens – Welcome aboard the journey into the world of education printable worksheets in Math, English, Science and Social Studies, Coordinated with the CCSS but Professionally applicable to Pupils of… Continue Reading →
5 Free Math Worksheets Third Grade 3 Multiplication Multiply Columns 1 Digit 4 Digit – Welcome aboard the journey to the world of education printable worksheets in Math, English, Science and Social Studies, aligned with the CCSS but Professionally applicable… Continue Reading →
4 Free Math Worksheets Third Grade 3 Place Value and Rounding Round 4 Digit Numbers Nearest 1000 – Welcome aboard the journey to the world of education printable worksheets in Math, English, Science and Social Studies, Coordinated with the CCSS… Continue Reading →
3 Free Math Worksheets Second Grade 2 Subtraction Single Digit Subtraction – Welcome aboard the journey to the world of education printable worksheets in Math, English, Science and Social Studies, Coordinated with the CCSS but Professionally applicable to Pupils of… Continue Reading →
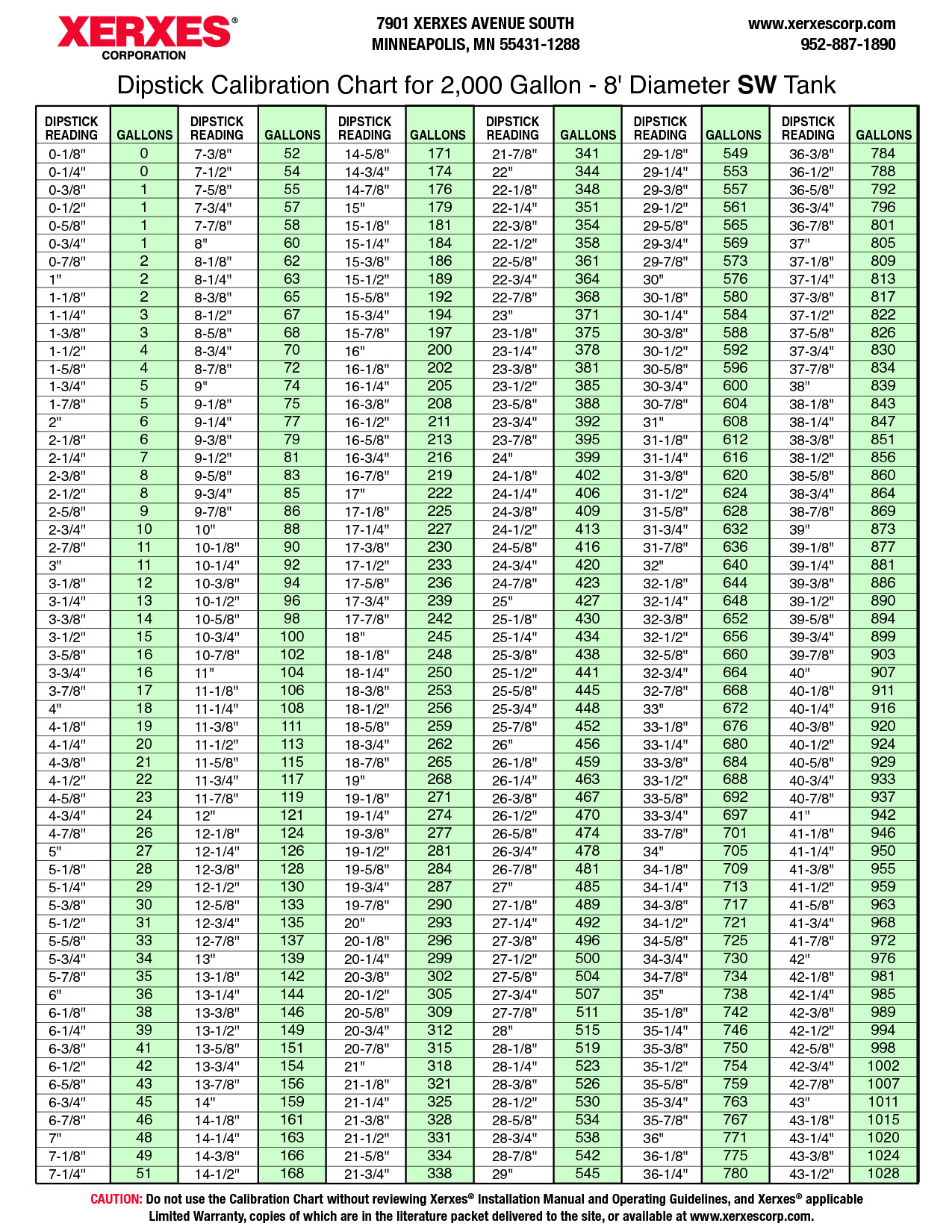
5 Free Math Worksheets Third Grade 3 Measurement Converting Cups Pints Quarts Gallons Hard – Welcome aboard the journey into the world of education printable worksheets in Math, English, Science and Social Studies, aligned with the CCSS but Professionally applicable… Continue Reading →
3 Free Math Worksheets Third Grade 3 Multiplication Multiply whole Tens – Welcome aboard the journey into the world of education printable worksheets in Math, English, Science and Social Studies, aligned with the CCSS but universally applicable to students of… Continue Reading →
4 Free Math Worksheets Second Grade 2 Skip Counting Skip Counting by 6 – Welcome aboard the journey into the world of education printable worksheets in Math, English, Science and Social Studies, Coordinated with the CCSS but Professionally applicable to… Continue Reading →
5 Free Math Worksheets Third Grade 3 Counting Money Counting Money Four Coins Plus One Five Ten Dollar – Welcome aboard the journey into the world of education printable worksheets in Math, English, Science and Social Studies, aligned with the… Continue Reading →
3 Free Math Worksheets Second Grade 2 Measurement Convert Yards Feet Inches Easy – Welcome aboard the journey to the world of education printable worksheets in Math, English, Science and Social Studies, Coordinated with the CCSS but universally applicable to… Continue Reading →